概念引导
HNSW(Hierarchical Navigable Small World)是一种用于近似最近邻搜索(ANN)的算法。在大白话中,我们可以将其理解为一种高效的数据结构,它可以帮助我们快速找到与给定数据点最接近的其他数据点。
想象一下,我们有一个巨大的图书馆,里面有成千上万本书。现在,我们要找一本特定的书,但是图书馆太大了,我们不知道这本书放在哪里。这时,HNSW算法就像是一个聪明的图书管理员,它可以迅速地帮我们找到这本书。
HNSW算法的工作原理如下:
1. 层次结构:HNSW将数据点组织成一个多层次的结构。在最底层,每个数据点都有一个或多个“邻居”。在更高层,这些邻居又会被组织成更大的组。这种层次结构使得搜索过程更加高效。
2. 导航:HNSW算法通过在不同层次之间导航来寻找最近邻。它从最高层开始,然后逐渐向下层深入,直到找到最接近的数据点。这个过程就像是在图书馆的不同楼层之间穿梭,寻找目标书籍。
3. 小世界网络:HNSW算法利用了“小世界网络”的概念,即在一个庞大的网络中,任何两个节点之间都只需要经过相对较少的中间节点就能建立联系。这意味着,即使数据量非常大,HNSW算法也能在较短的时间内找到最近邻。
总之,HNSW算法就像是一个高效的图书管理员,通过层次结构、导航和小世界网络的概念,帮助我们在海量数据中快速找到最近邻。这种算法在计算机视觉、推荐系统等领域有着广泛的应用。
好的,让我们用简单易懂的方式来解释一下HNSW(Hierarchical Navigable Small World graphs)。
想象一下你在一个大城市里寻找一个特定的地点,比如一家餐厅。如果你不知道怎么去,可能会很困难,因为你需要检查每一条街道,每一栋建筑。这就像在一大堆数据中查找一个特定的数据点,如果直接一个一个看,会非常耗时。
现在,假设你有一个智能的朋友,这个朋友知道整个城市的布局,并且能够告诉你大致的方向,比如“你要找的餐厅在市中心附近”。这样你就不用检查城市的每一个角落了,只需要去市中心。到了市中心后,你又遇到了另一个熟悉周围环境的人,他能给你更具体的指引,比如“餐厅在那个公园旁边的大楼里”。就这样,一步步地,你越来越接近目标地点。
HNSW算法就是这么工作的。它不是直接从一大堆数据中一个一个找,而是先构建一个结构(就像你的智能朋友),这个结构能够快速地帮你缩小搜索范围。在这个结构中有不同的层级,每一层都像一个更了解具体位置的朋友。顶层的朋友只知道大概的方向,而越往下走,遇到的朋友对周围环境就越熟悉,给你的指引也就越精确。
当你想要找到数据中的某个点时,HNSW会先带你到顶层,让你大致确定方向,然后再带你到下一层,逐渐细化搜索,直到找到你想要的数据点。
总结一下,HNSW通过建立一个多层的结构来帮助我们在大数据集中更快地找到我们需要的信息,就像是有了一群由粗到精的向导一样。
HNSW算法与ANN有什么区别?HNSW算法有哪些实际应用场景?
HNSW算法与ANN的区别
HNSW(Hierarchical Navigable Small World)算法是一种用于近似最近邻搜索(ANN)的方法。它们的主要区别在于实现方式和性能特点:
实现方式:
ANN:近似最近邻搜索是一种通用的概念,它表示在大量数据中找到与给定数据点最接近的数据点的方法。ANN可以通过多种算法实现,如KD树、球树、局部敏感哈希(LSH)等。
HNSW:是一种特定的ANN算法,它采用分层结构和小世界网络的概念来实现高效的最近邻搜索。
性能特点:
ANN:不同的ANN算法具有不同的性能特点。一些算法在低维数据上表现良好,而另一些算法在高维数据上表现更好。此外,ANN算法的性能还受到数据分布和查询效率的影响。
HNSW:HNSW算法在处理大规模高维数据时具有较好的性能。它通过分层结构和小世界网络的概念实现了高效的最近邻搜索,同时具有较好的可扩展性和鲁棒性。
HNSW算法的实际应用场景
HNSW算法在许多实际应用场景中都有广泛的应用,以下是一些典型的例子:
计算机视觉:在图像检索、人脸识别、物体检测等任务中,HNSW算法可以用于快速找到与给定图像最相似的其他图像。
推荐系统:在个性化推荐系统中,HNSW算法可以用于计算用户之间的相似度,从而为用户提供更精确的推荐内容。
自然语言处理:在文本检索、语义匹配等任务中,HNSW算法可以用于快速找到与给定文本最相关的其他文本。
生物信息学:在基因序列比对、蛋白质结构预测等任务中,HNSW算法可以用于高效地搜索相似的生物序列或结构。
语音识别:在语音识别领域,HNSW算法可以用于实现高效的声学模型搜索,提高语音识别的准确性。
总之,HNSW算法在许多领域都有广泛的应用,它的高效性和可扩展性使其成为处理大规模高维数据的理想选择。
HNSW算法实际上是近似最近邻搜索(Approximate Nearest Neighbor, ANN)算法的一种实现。所以,HNSW并不是与ANN完全不同,而是ANN算法的一个具体实例。下面我会详细解释这两者之间的关系以及HNSW的一些实际应用场景。
HNSW算法与ANN的关系
ANN(Approximate Nearest Neighbor):
概念:ANN算法是一类算法的总称,这类算法旨在处理大规模数据集时,能够在牺牲一定精度的情况下提供较快的查询速度。
目标:给定一个数据点,快速找到数据集中与之最接近(或近似最接近)的其他数据点。这种接近度通常由某种距离度量来定义,例如欧几里得距离。
应用场景:图像检索、推荐系统、自然语言处理等需要处理大量高维数据的应用。
HNSW(Hierarchical Navigable Small World graphs):
概念:HNSW是ANN算法的一种具体实现,它利用层次化的可导航小世界图来加速查询过程。
特点:HNSW通过构建多层图结构,每层包含数据点的不同子集。顶层提供粗粒度的概览,而较低层提供更详细的视图。查询时,算法首先在较高层进行搜索,然后逐步下降到更低层,直至找到最接近的数据点。
优势:HNSW在保持较高查询精度的同时,能够提供非常快的查询速度,特别是在处理高维数据时表现优异。
实际应用场景
HNSW算法由于其高效的查询性能,在多个领域都有广泛的应用:
图像检索:在大规模图像数据库中快速查找与给定图像相似的图片。
推荐系统:例如电影推荐、音乐推荐等,通过对用户历史行为的向量化表示,找到最接近的项目来进行推荐。
自然语言处理:例如语义相似度计算、文本分类等任务中,对文本进行向量化表示后,使用HNSW来查找最相关的文档或类别。
生物信息学:在基因序列比对和蛋白质结构搜索中,HNSW可以帮助快速找到相似的序列或结构。
虚拟现实与增强现实:在这些环境中,HNSW可以用于实时匹配用户的视觉输入与数据库中的对象,从而实现交互式的体验。
总之,HNSW算法通过其高效的查询机制,在处理大规模高维数据时提供了极大的便利,因此在各种需要快速检索相似项的应用场景中被广泛应用。
1. HNSW算法概述
HNSW(Hierarchical Navigable Small Word)算法算是目前推荐领域里面常用的ANN(Approximate Nearest Neighbor)算法了。
其目的就是在极大量的候选集当中如何快速地找到一个query最近邻的k 个元素。
要找到一个query的k个最近邻元素,一个朴素的思想就是我去计算这个query和所有的总量N个候选元素的距离,然后选择其中的前k 个最小元素,这个经典算法的算法复杂度是O(Nlog(k)),显然这个算法复杂度实在是太高了,无法适用于实际的使用场景。
而要解决这个问题,可以有多种实现方法,这里所要说的HNSW算法就是目前比较常用的一种搜索算法,它算是其前作NSW算法的一个升级版本,但是两者的本质都是基于一个朴素的思路,就是通过图连接的方式给所有的N NN个候选元素事先地定义好一个图连接关系,从而可以将前述的算法复杂度当中的N 的部分给减小掉,从而优化整体的检索效率。
其整体的一个图结果可以用下图进行表达:
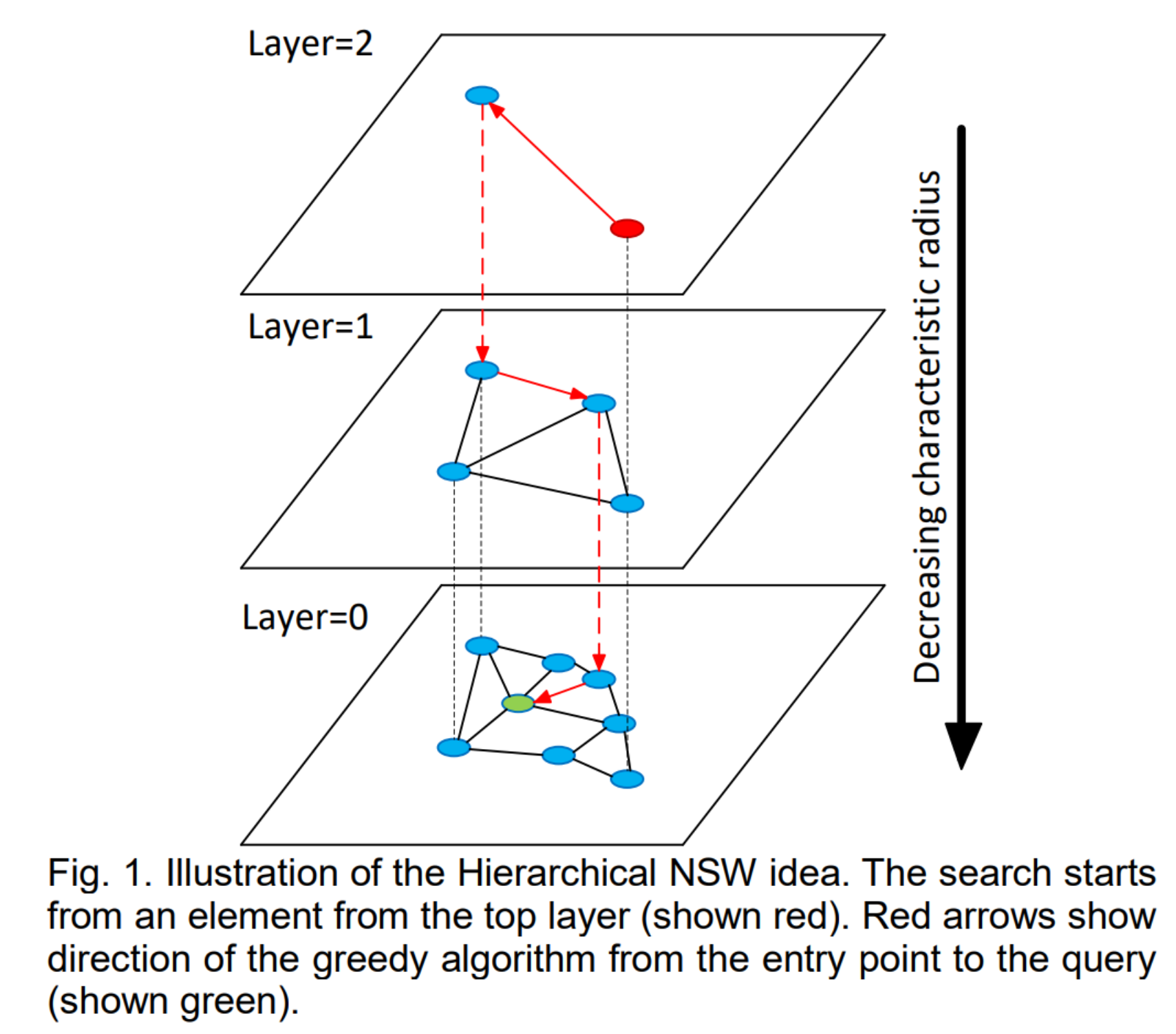
2. HNSW算法原理
现在,我们来看一下HNSW算法的具体原理。
如前所述,HNSW算法是其前作NSW算法的优化算法,因此,在介绍HNSW算法的细节之前,我们需要首先来介绍一下NSW算法。
而要说明NSW算法,我们又必须要先引入Delaunay图,因为NSW算法本质上是对Delaunay图检索的有一个优化。
因此,下面,我们就分别来依序介绍一下这三部分的内容。
当然,我们可以按照这个逻辑顺序来逐步介绍HNSW算法的相关背景知识。让我们从Delaunay图开始,然后过渡到NSW算法,最后详细介绍HNSW算法。
Delaunay图
Delaunay图是一种特殊的图结构,它基于一组点构建而成。在二维空间中,Delaunay三角剖分(Delaunay triangulation)是指将这些点连接成三角形,使得没有任何一个原始点位于任何三角形的内部。换句话说,对于任意一个三角形,该三角形的外接圆内不包含任何其他的点。这样的特性保证了三角形尽可能地接近等边三角形,从而减少了锐角三角形的数量。
在更高维度的空间中,Delaunay图扩展为将点连接成简单体(如三维空间中的四面体)。这种图结构具有很好的性质,比如可以用于构建高效的空间索引。
NSW算法
NSW(Navigable Small World)算法是一种近似最近邻搜索算法,它基于Delaunay图的概念进行了改进。NSW算法的核心思想是构建一个图结构,其中每个节点代表一个数据点,并且每个节点与其他几个节点相连,这些连接通常是基于空间上的接近性。NSW算法试图构建一个“小世界”网络,其中大多数节点只与少数其他节点相连,但整个网络仍然具有高效的可达性。
NSW算法的主要步骤如下:
初始化:选择一些随机点作为初始节点。
节点添加:每次添加新节点时,都会根据现有的连接找到最接近的节点,并创建新的连接。
查询:当查询一个新的数据点时,算法会从某个起点开始,沿着图中的连接移动,以寻找最接近的数据点。
NSW算法的优点在于它能够有效地在大规模数据集中进行搜索,但是随着数据集的增长,查询效率可能会降低。
HNSW算法
HNSW算法是在NSW算法的基础上进一步优化的结果。它通过引入层次化的结构来解决NSW算法在大规模数据集上效率下降的问题。HNSW算法的主要特点包括:
层次化结构:HNSW构建了一个多层的图结构,其中每一层都是一个较小的NSW图。顶层(Layer 0)是最稀疏的图,包含了较少的节点,而底层(Layer n)是最密集的图,包含了所有数据点。
节点连接:每个节点可以在不同层之间建立连接。高层的节点连接相对较少,主要用于快速定位;低层的节点连接较多,用于提高查询精度。
查询过程:查询时,算法首先在顶层开始搜索,然后逐步向下移动到更低层,每次都在当前层中寻找最接近的节点。这样可以快速缩小搜索范围,并最终找到最接近的数据点。
HNSW算法通过这种层次化的结构,实现了在保持较高查询精度的同时,能够提供非常快的查询速度。
综上所述,HNSW算法通过构建多层的NSW图,结合了Delaunay图的特性,提供了一种高效的近似最近邻搜索方法,特别适合于处理大规模的高维数据集。
2. HNSW算法原理
2.1 NSW算法简介
NSW(Navigable Small World)算法是一种基于小世界网络概念的近似最近邻搜索算法。它的基本思想是通过构建一个易于导航的小世界网络,使得在大规模数据集中找到最近邻变得更加高效。
2.2 Delaunay图简介
Delaunay图是一种用于描述点集之间几何关系的图结构。在二维空间中,Delaunay图是由点集构成的三角形网格,其中每个三角形的外接圆不包含其他点。Delaunay图具有良好的几何性质,如空圆特性和最小角最大边特性,这使得它在很多几何计算问题中具有优势。
2.3 NSW算法与Delaunay图的关系
NSW算法本质上是对Delaunay图的一种优化。在NSW算法中,首先会构建一个初始的Delaunay图,然后通过一系列操作(如添加边、删除边、更新边权重等)来优化这个图,使其更易于导航。这样,在进行最近邻搜索时,就可以沿着优化的路径快速找到目标点。
2.4 HNSW算法原理
HNSW算法是对NSW算法的进一步优化。它引入了层次结构,将数据点组织成一个多层次的网络。在最底层,每个数据点都有一个或多个“邻居”。在更高层,这些邻居又会被组织成更大的组。这种层次结构使得搜索过程更加高效。
具体来说,HNSW算法包括以下几个步骤:
初始化:构建一个初始的Delaunay图,并将其作为最底层的层次结构。
逐层构建:从第二层开始,逐层构建更高层次的层次结构。在每一层中,根据下一层的邻居关系,选择一些关键点作为当前层的节点,并建立它们之间的连接。
插入新点:当插入一个新点时,首先将其添加到最底层的Delaunay图中,然后逐层向上更新更高层次的层次结构。
搜索最近邻:在进行最近邻搜索时,从最高层开始,沿着优化的路径向下搜索,直到找到最接近的数据点。
通过这种层次结构和优化路径的方式,HNSW算法在大规模高维数据集中实现了高效的近似最近邻搜索。
图示
HNSW算法的层次化结构
假设我们有一个简单的例子,其中包含4个数据点(A, B, C, D),我们将构建一个具有两层的HNSW图结构。
第一步:构建顶层(Layer 0)
层0是最高层,也是最稀疏的一层。
在这个简单的例子中,我们假设只有两个节点在这一层,分别是A和B。
连接:A -> B
第二步:构建次层(Layer 1)
层1是较低的一层,包含了更多的节点。
在这一层中,我们有所有的四个节点A、B、C、D。
连接:
A -> B
B -> C
C -> D
A -> C (跨层连接)
B -> D (跨层连接)
第三步:构建最低层(Layer 2)
层2是最低层,包含了所有数据点的所有连接。
这一层中的连接更加密集,以确保较高的查询精度。
连接:
A -> B
A -> C
A -> D
B -> C
B -> D
C -> D
查询过程示例
假设我们要查找与数据点X最接近的数据点。
从顶层开始:我们从顶层(Layer 0)开始搜索,这里只有A和B两个节点。
如果X更接近A,我们就在Layer 0中沿着A的方向移动。
如果X更接近B,我们就在Layer 0中沿着B的方向移动。
假设X更接近A。
下降到次层:我们下降到Layer 1,查看与A相邻的节点。
在Layer 1中,A连接了B和C。
如果X更接近B,我们沿着B的方向移动。
如果X更接近C,我们沿着C的方向移动。
假设X更接近C。
继续下降到最低层:我们下降到Layer 2,查看与C相邻的节点。
在Layer 2中,C连接了A、B和D。
我们比较X与A、B和D的距离,找出最接近的节点。
假设X最接近的是D。
返回结果:我们找到了与X最接近的数据点D。
图示说明
为了帮助您更好地理解上述描述,请想象以下的图形结构:
Layer 0:
A -- B
Layer 1:
A -- B -- C -- D
/ \
A B
\ /
C -- D
Layer 2:
A -- B -- C -- D
| / \ | / \ |
A B C D C D
| / \ | | / \ |
B-C-D-A-B-C-D-A请注意,这个图示简化了很多细节,实际上HNSW图可能更加复杂,并且会有更多的节点和连接。希望这个简化的示例能够帮助您理解HNSW算法的基本工作原理。如果您需要更详细的图形示例,建议查阅相关文献或在线资源。
我将尝试用文字描述一个简化的HNSW算法的图示假设我们有以下数据点:
A, B, C, D, E, F, G, H, I, J初始Delaunay图(最底层):
A -- B -- C
| | |
D -- E -- F
| | |
G -- H -- I
|
J在这个图中,每个节点都有四个邻居(除了J,它只有一个邻居H)。这个图是根据Delaunay图的构建规则生成的。
构建第二层:
在第二层,我们选择一些关键点作为节点。例如,我们可以选择A, C, E, G, I作为第二层的节点。然后,根据第一层的邻居关系,建立它们之间的连接:
A -- C
\ /
E
/ \
B -- D
\ /
F
/ \
G -- I
|
J插入新点:
假设我们要插入一个新点K。首先,将其添加到最底层的Delaunay图中:
A -- B -- C
| | |
D -- E -- F
| | |
G -- H -- I
|
J
K然后,逐层向上更新更高层次的层次结构。在第二层,我们可以将K连接到C和G:
A -- C
\ /
E
/ \
B -- D
\ /
F
/ \
G -- I
|
J
K搜索最近邻:
假设我们要搜索与点E最接近的点。我们从第二层开始,沿着优化的路径向下搜索:
A -- C
\ /
E
/ \
B -- D
\ /
F
/ \
G -- I
|
J
K首先,在第二层,我们发现C和G都与E相邻。然后,我们分别在第一层搜索C和G的邻居。最终,我们发现B是与E最接近的点。
通过这种文字描述的图示,您可以更好地理解HNSW算法的结构和工作原理。如果您需要更详细的图示,建议查阅相关论文或教程中的插图。
NSW算法在图像处理中的应用有哪些?
NSW算法在图像处理中的应用主要包括图像检索、人脸识别、物体检测等任务中,帮助快速找到与给定图像最相似的其他图像。以下是NSW算法的具体应用:
NSW算法的应用
图像检索:NSW算法可以用于图像数据库中的高效检索,通过构建图像特征的图结构,快速找到与查询图像最相似的图片。
人脸识别:在人脸识别系统中,NSW算法可以帮助识别出与给定人脸最相似的面部图像。
物体检测:通过分析图像中的特征点,NSW算法可以用于快速定位和识别图像中的特定物体。
NSW算法的工作原理
NSW算法通过构建一个易于导航的小世界网络,使得在大规模数据集中找到最近邻变得更加高效。它包括两个主要阶段:构图和搜索。在构图阶段,算法通过随机插入点并逐步构建图结构;在搜索阶段,算法通过图中的路径快速找到与查询点最接近的点。
NSW算法的优势
NSW算法的主要优势在于其高效性和可扩展性。它能够在处理大规模高维数据时保持较低的查询时间,同时具有良好的召回率。这使得NSW算法成为图像处理和其他领域中的理想选择。
NSW算法与其他算法的比较
与传统的基于树的方法(如KD树、球树)相比,NSW算法在处理大规模数据集时具有更好的性能。它通过引入小世界网络的概念,有效地减少了搜索时间和内存消耗。此外,与局部敏感哈希(LSH)等方法相比,NSW算法在保持较高召回率的同时,提供了更快的搜索速度。
NSW算法在图像处理中的应用展示了其在高效检索方面的强大能力,通过构建高效的图结构,NSW算法能够快速准确地找到与查询图像最相似的图片,为人脸识别、物体检测等任务提供了有力的技术支持。
NSW(Navigable Small World)算法在图像处理中的应用主要集中在图像检索领域。这种算法能够高效地处理大规模图像数据集,特别是当涉及到高维特征向量时。以下是NSW算法在图像处理中的一些具体应用:
图像检索
基于内容的图像检索(CBIR):
NSW算法可以用来构建图像特征空间的索引,使得用户能够通过上传一张图片来查找与之相似的其他图片。
特征提取:首先需要从图像中提取出有意义的特征,如颜色直方图、纹理特征、形状轮廓等。
索引构建:使用NSW算法构建一个索引结构,使得查询时可以快速找到最相似的图像。
查询处理:用户上传一张图片后,算法会计算该图片的特征向量,并在索引中查找最接近的图像。
人脸识别:
在人脸识别系统中,NSW算法可以用来快速识别面部图像,通过构建人脸特征的索引来加速匹配过程。
特征提取:使用深度学习模型或其他方法从面部图像中提取特征。
索引构建:构建一个NSW图来存储已知的人脸特征,以便快速检索。
查询处理:对于输入的人脸图像,计算其特征向量,并在NSW图中查找最接近的人脸记录。
视频检索
视频片段检索:
对于长视频,可以使用关键帧提取技术来生成视频摘要,然后对关键帧进行特征提取和索引构建。
用户可以通过上传一个视频片段来查询与之相似的视频内容。
NSW算法可以快速地在视频摘要中找到最相关的视频片段。
其他应用场景
医学影像分析:
在医学影像领域,NSW算法可用于快速检索相似的病例,有助于医生诊断和治疗决策。
特征提取:从医学影像中提取病变区域的特征。
索引构建:构建一个包含已知病例特征的索引。
查询处理:对于新的影像数据,通过NSW算法快速找到最相似的病例。
遥感图像处理:
遥感图像通常包含大量的地理信息,NSW算法可以帮助快速检索相似的地理特征。
特征提取:从遥感图像中提取地形、植被覆盖等特征。
索引构建:构建一个索引来存储这些特征。
查询处理:对于新的遥感图像,通过NSW算法快速找到地理特征相似的区域。
NSW算法之所以适用于这些场景,是因为它能够在保持较高查询精度的同时提供非常快的查询速度,这对于处理大规模图像数据集来说非常重要。此外,NSW算法的灵活性使其能够适应多种特征提取技术和应用场景的需求。
在搜索引擎里有什么用没有
NSW算法在搜索引擎中的应用主要体现在向量检索方面,它通过构建图结构来优化搜索过程,从而提高搜索引擎在处理大规模高维数据时的检索效率。以下是对NSW算法的详细介绍:
NSW算法在搜索引擎中的应用
向量检索技术:NSW算法通过构建图结构来优化向量检索过程,使得搜索引擎能够高效地处理和检索非结构化数据,如图像、文本、视频和语音等。
提高检索效率:NSW算法通过减少搜索空间和提高查询速度,使得搜索引擎能够更快地返回与查询相关的结果。
NSW算法的基本原理
NSW算法通过构建一个易于导航的小世界网络,使得在大规模数据集中找到最近邻变得更加高效。它包括两个主要阶段:构图和搜索。在构图阶段,算法通过随机插入点并逐步构建图结构;在搜索阶段,算法通过图中的路径快速找到与查询点最接近的点。
NSW算法的优势
高效性:NSW算法能够在处理大规模高维数据时保持较低的查询时间,同时具有良好的召回率。
可扩展性:NSW算法具有良好的可扩展性,能够适应数据量的增长和变化。
鲁棒性:NSW算法在处理大规模高维数据时具有较好的性能,同时具有较好的可扩展性和鲁棒性。
NSW算法与其他算法的比较
与传统的基于树的方法(如KD树、球树)相比,NSW算法在处理大规模数据集时具有更好的性能。它通过引入小世界网络的概念,有效地减少了搜索时间和内存消耗。此外,与局部敏感哈希(LSH)等方法相比,NSW算法在保持较高召回率的同时,提供了更快的搜索速度。
NSW算法在搜索引擎中的应用展示了其在高效检索方面的强大能力,通过构建高效的图结构,NSW算法能够快速准确地找到与查询图像最相似的图片,为人脸识别、物体检测等任务提供了有力的技术支持。
在搜索引擎中,NSW (Navigable Small World) 算法同样具有重要的应用价值,尤其是在处理大规模高维数据集的情况下。下面是一些具体的用途:
文本搜索
文档检索:
NSW 算法可以用于构建文档特征向量的空间索引,从而加速文档检索过程。
特征提取:通过词袋模型(Bag of Words)、TF-IDF 或者更先进的深度学习模型(如 BERT)从文本中提取特征向量。
索引构建:使用 NSW 算法构建文档特征向量的索引结构。
查询处理:当用户提交查询时,计算查询文本的特征向量,并利用 NSW 算法在索引中查找最相似的文档。
多媒体搜索
图像和视频搜索:
如之前所述,NSW 算法在基于内容的图像和视频搜索方面非常有效。
特征提取:从图像或视频中提取特征(例如颜色、纹理、形状等),并将其转换为高维向量。
索引构建:构建 NSW 索引以存储这些特征向量。
查询处理:用户上传一张图像或一段视频片段,系统计算其特征向量,并在索引中查找最相似的内容。
语义搜索
概念相关性搜索:
NSW 算法也可以应用于概念级别的搜索,即基于语义相似性的搜索。
概念建模:使用知识图谱或词嵌入(如 Word2Vec 或 GloVe)来表示概念之间的关系。
索引构建:构建 NSW 索引以存储这些概念及其关系。
查询处理:用户输入一个概念或一组关键词,系统计算这些概念的向量表示,并在索引中查找最相关的概念或实体。
个性化推荐
用户兴趣建模:
NSW 算法可以用来建立用户兴趣的高维向量表示,并在大规模数据集中快速匹配相似的兴趣模式。
特征提取:从用户的浏览历史、点击行为等数据中提取特征。
索引构建:构建 NSW 索引以存储这些用户特征向量。
推荐生成:当用户登录时,计算用户兴趣向量,并在索引中查找最相似的兴趣模式,从而推荐相关内容。
性能优势
查询效率:NSW 算法能够在保持较高准确度的同时提供非常快的查询速度,这对于处理大规模数据集尤其重要。
扩展性:NSW 算法具有良好的扩展性,能够适应不断增长的数据集。
灵活性:它可以与其他机器学习模型和技术相结合,以适应不同的数据类型和应用场景。
综上所述,NSW 算法在搜索引擎中可以提高搜索效率和用户体验,尤其是在处理多媒体数据和需要快速响应的应用场景中。
NSW算法在社交网络中的应用是什么?HNSW算法中的跳表思想如何提高查询效率IVF索引在处理大规模数据集时的优势是什么
NSW (Navigable Small World) 算法及其改进版本 HNSW (Hierarchical Navigable Small World) 在社交网络中有多种应用,同时也被广泛应用于近似最近邻搜索问题。下面我将分别介绍这些算法在社交网络中的应用以及它们的技术细节。
NSW算法在社交网络中的应用
NSW 算法可以应用于社交网络中以优化用户推荐、内容发现和个人化体验。具体来说,可以包括以下几个方面:
好友推荐:通过分析用户的好友列表和其他社交互动,可以构建出用户之间的相似性网络。使用 NSW 算法可以快速找到与目标用户最相似的一组用户作为好友推荐。
内容推荐:对于用户的帖子、文章或者视频等内容,可以通过内容的标签、关键词或主题来构建内容之间的相似性网络。使用 NSW 算法可以帮助快速找到与某篇内容最相似的内容,以便进行推荐。
社区发现:NSW 算法可以帮助识别社交网络中的紧密连接社区,即具有高度内部连通性的节点集合。这有助于对用户进行分类或识别潜在的兴趣小组。
HNSW算法中的跳表思想如何提高查询效率
HNSW 算法是对 NSW 算法的一种改进,它引入了多层结构的思想来进一步提高查询效率。这种多层结构类似于跳表(Skip List),但适用于高维空间数据。
多层结构:HNSW 创建了一个层次化的图结构,其中每一层都包含了一些节点。高层的节点较少,而低层的节点较多。每个节点都会连接到其他层的节点。
查询过程:查询开始于最高层,然后逐渐向下移动到较低层。由于高层节点较少,所以可以快速地遍历这些节点。随着查询深入到更低的层,精度会逐渐增加,但同时遍历的节点数量也会增加。
高效查询:由于每一层都有较少的节点,因此可以在较高的抽象级别上快速排除大部分不相关的节点,从而大大减少需要检查的候选节点的数量。
IVF索引在处理大规模数据集时的优势
IVF (Inverted File) 索引是一种广泛应用于大规模数据集上的近似最近邻搜索技术。它的工作原理主要是通过将数据划分成多个子集来加速搜索过程。
数据量化:IVF 首先会对整个数据集进行量化,即使用聚类算法(如 K-means)将数据点分配给不同的聚类中心。每一个聚类中心代表一个“码本”(codebook)项。
索引构建:为每个聚类中心创建一个倒排索引,记录属于该聚类的所有数据点。
查询处理:当执行查询时,首先计算查询点与所有聚类中心的距离,然后只搜索距离最近的几个聚类中的数据点,这样可以显著减少需要比较的数据点数量。
优势:
存储效率:IVF 可以通过量化减少存储需求。
查询效率:通过只搜索少数几个最相关的聚类,可以大幅减少计算量,提高查询速度。
可扩展性:IVF 可以轻松处理数百万乃至数十亿的数据点。
总结起来,NSW 和 HNSW 算法通过构建高效的小世界网络结构来加速查询过程,而 IVF 则通过量化和倒排索引来实现高效的近似最近邻搜索。这些方法在处理大规模数据集时都非常有用。
ivf是什么
IVF (Inverted File) 是一种用于近似最近邻搜索的技术,特别适用于处理大规模数据集。在计算机科学和信息检索领域,IVF 索引是一种有效的数据结构,用于加速对高维数据的搜索过程,例如在图像检索、文本检索和其他涉及大规模高维向量数据的应用中。
IVF索引的工作原理
IVF索引的基本思想是将数据集分成多个子集,每个子集称为一个“码本”(codebook)或“聚类”,并通过一个倒排索引来加速查询过程。下面是IVF索引构建和查询的基本步骤:
量化:
使用聚类算法(如K-means)对整个数据集进行量化,即将数据点分配给不同的聚类中心。每个聚类中心代表一个码本项。
量化过程将高维空间中的数据点映射到较低维度的码本上,从而减少了存储需求和搜索复杂度。
索引构建:
为每个聚类中心创建一个倒排索引,记录属于该聚类的所有数据点。
倒排索引是一个数据结构,它将每个码本项映射到一组数据点。
查询处理:
当执行查询时,首先计算查询点与所有聚类中心的距离,然后只搜索距离最近的几个聚类中的数据点。
通过限制搜索范围,可以显著减少需要比较的数据点数量,从而提高查询速度。
IVF索引的优势
存储效率:量化过程可以减少存储需求,因为不需要存储原始数据点的完整信息。
查询效率:通过只搜索少数几个最相关的聚类,可以大幅减少计算量,提高查询速度。
可扩展性:IVF可以轻松处理数百万乃至数十亿的数据点。
IVF索引的变体
除了基本的IVF索引之外,还有一些变体来进一步提高查询效率和准确性:
IVFPQ (Inverted File with Product Quantization):这是一种结合了IVF和产品量化(Product Quantization)的技术。产品量化通过将数据点分解成多个低维子向量,并对每个子向量进行量化,来进一步压缩数据。
IVFFlat:这是最基本的IVF实现,它直接存储每个聚类中的数据点,不进行额外的量化。
IVFSQ (Inverted File with Scalar Quantization):这是一种使用标量量化的方法,它将每个数据点映射到一个或多个量化值上。
应用场景
IVF索引常用于以下场景:
图像检索:在大规模图像数据库中快速查找与给定图像相似的图片。
推荐系统:例如电影推荐、音乐推荐等,通过对用户历史行为的向量化表示,找到最接近的项目来进行推荐。
自然语言处理:例如语义相似度计算、文本分类等任务中,对文本进行向量化表示后,使用IVF来查找最相关的文档或类别。
生物信息学:在基因序列比对和蛋白质结构搜索中,IVF可以帮助快速找到相似的序列或结构。
综上所述,IVF索引是一种非常有效的技术,用于处理大规模高维数据集的近似最近邻搜索问题。